

يجب التصريح عن نوع كل متغير في اللغة التي يحدَّد فيها نوع المتغير typed language مثل اللغة C، إذ يُعلِم النوع المصرِّف مالذي يتوقع تخزينه في المتغير، وبالتالي يستطيع المصرّف تخصيص مساحة كافية لهذا الاستخدام، والتحقق من أن المبرمج لا ينتهك قيود النوع المحدَّد
معايير اللغة C
من الضروري الاطلاع قليلًا على تاريخ اللغة البرمجية C على الرغم من الاختلاف الطفيف بينها وبين بقية اللغات، إذ تُعَدّ C بأنها اللغة السائدة في عالم برمجة الأنظمة، فكل نظام تشغيل ومكتباته المرتبطة به التي يشيع استخدامها مكتوبة باللغة C، كما يوفِّر كل نظام مصرِّفًا compiler للغة C، وقد وضِع معيار صارم لهذه اللغة للحد من اختلافها بين هذه الأنظمة والتي من المؤكد أنّ كل منها سيجري العديد من التغييرات التي لن تتوافق مع بعضها.
يُعرَف هذا المعيار رسميًا باسم ISO/IEC 9899:1999(E)، لكن يشار إليه عادةً بالاختصار C99، إذ تشرف عليه منظمة المعايير الدولية ISO، كما أتيح شراء المعيار كاملًا على الإنترنت، ولم تَعُد الإصدارات القديمة من هذا المعيار مثل الإصدار C89 -الذي سبق C99 وأصدِر في عام 1989- و ANSI C شائعة الاستخدام، وأصبحت جزءًا من أحدث معيار، كما أنّ توثيق المعيار تقني بحت ويذكر بالتفصيل تقريبًا جميع نواحي اللغة، إذ يشرح مثلًا بنيتها بصيغة باكوس نور Backus Naur وقيم define# المعيارية والآلية التي يجب أن تعمل وفقها العمليات.
من الضروري أيضًا ملاحظة ما الذي لا تحدده معايير اللغة C، والأهم من ذلك أنه يجب أن يكون المعيار ملائمًا لكل معمارية حاسوبية حالية ومستقبلية، وبالتالي يحرص على عدم تحديد المجالات التي تعتمد على المعمارية، كما يُعَدّ الرابط بين معيار اللغة C والمعمارية الأساسية هو واجهة التطبيق الثنائية Application Binary Interface -أو ABI اختصارًا- التي سنتحدث عنها لاحقًا، كما سيذكر المعيار في عدة مواضع أن أية عملية أو بنية معيّنة سيكون لها نتيجة غير محددة أو نتيجة تعتمد على التنفيذ، ومن البديهي أن المبرمج لا يمكنه الاعتماد على هذه النتائج إذا كان يريد كتابة شيفرة برمجية محمولة portable.
جنو سي GNU C
ينفِّذ مصرِّف GNU C -والذي يشار إليه عادةً بالاختصار gcc- معيار C99 بالكامل تقريبًا، ويطبِّق أيضًا مجموعة إضافات للمعيار سيستخدمها المبرمجون غالبًا للحصول على خصائص وظيفية إضافية على حساب قابلية النقل إلى مصرِّف آخر، إذ ترتبط هذه الإضافات عادةً بالشيفرة البرمجية ذات المستوى المنخفض low level code وهي أكثر شيوعًا في مجال برمجة النظم؛ أما أكثر إضافة يشيع استخدامها في هذا المجال، فهي شيفرة التجميع المُضمّن inline assembly، كما يجب على المبرمجين قراءة توثيق مصرِّف GNU C وفهم متى قد يستخدِمون الخصائص الإضافية على المعيار.
يمكن توجيه مصرِّف GNU C للالتزام بدقة بالمعيار مثل راية std = c99- والتحذير أو توليد خطأ عند تنفيذ أمور معينة لا تتوافق مع المعيار. وهذا طبعًا يناسبك عندما تكون بحاجة إلى ضمان إمكانية نقل شيفرتك البرمجية بسهولة إلى مصرِّف آخر.
الأنواع
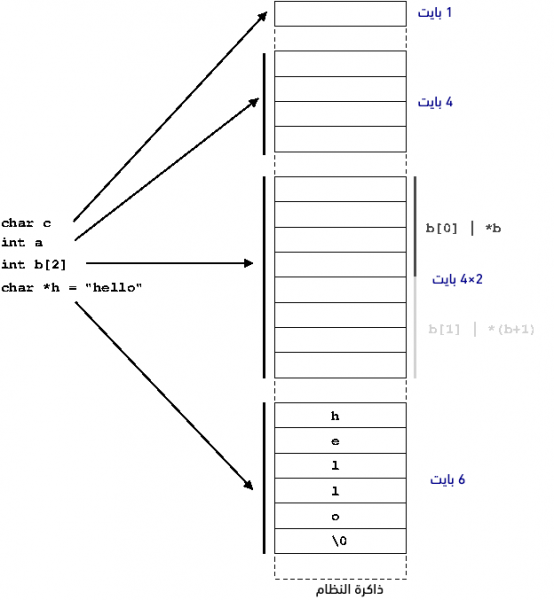
نحن المبرمجون معتادون على استخدام المتغيرات لتمثيل مساحة من الذاكرة لتحمل قيمةً، إذ يجب التصريح عن نوع كل متغير في اللغة التي يُحدَّد فيها نوع المتغير typed language مثل اللغة C، كما يخبر النوع المصرِّف مالذي يتوقع تخزينه في المتغير، وبالتالي سيستطيع المصرِّف تخصيص مساحة كافية لهذا الاستخدام والتحقق من أنّ المبرمج لا ينتهك قيود النوع المحدَّد، وسنجد في الصورة التالية مثالًا على المساحة المخصصة لبعض الأنواع الشائعة من المتغيرات.
(الأنواع)
يذكر معيار C99 أصغر حجم ممكن لكل نوع من أنواع المتغيرات المعرَّفة في اللغة C فقط، وذلك لأنّ الحجم الأمثل للأنواع يختلف اختلافًا كبيرًا بين مختلف معماريات المعالجات وأنظمة التشغيل، ولكي تكون العملية صحيحةً تمامًا يجب ألا يفترض المبرمجون أبدًا حجم أيّ من متغيراتهم، لكن يحتاج نظام التشغيل الفعال بطبيعة الحال إلى اتفاقات حول الأحجام التي ستحجزها أنواع المتغيرات في النظام، كما تتقيد كل معمارية ونظام تشغيل بواجهة التطبيق الثنائية Application Binary Interface -أو ABI اختصارًا-، إذ تملأ واجهة التطبيق الثنائية لنظام ما التفاصيل التي تربط بين معيار اللغة C ومتطلبات العتاد الصلب الأساسي ونظام التشغيل، كما تُكتَب واجهة التطبيق الثنائية لمجموعة محدَّدة من المعالج ونظام التشغيل.
| النوع | الحجم الأدنى وفق معيار C99 بواحدة البِتّ | الحجم الشائع أي معمارية 32 بِتّ |
|---|---|---|
| char | 8 | 8 |
| short | 16 | 16 |
| int | 16 | 32 |
| long | 32 | 32 |
| long long | 64 | 64 |
| المؤشرات Pointers | حسب التنفيذ | 32 |
نلاحظ في مثالنا السابق أنّ الاختلاف الوحيد عن المعيار C99 هو أن حجم المتغير من نوع int هو 32 بِتّ عادةً، وهو ضعف الحد الأدنى الصارم لحجم 16 بت الذي يتطلبه المعيار C99، كما أنّ المؤشرات Pointers هي فعليًا عنوان فقط، أي أنّ قيمتها تكون عنوانًا وبالتالي "تشير" إلى موقع آخر في الذاكرة، لذا يجب تخصيص حجم كافٍ للمؤشر حتى يتمكن من عنونة أيّ موقع في ذاكرة النظام.
64 بت
إحدى النواحي المربِكة هي إدراج حوسبة 64 بت، إذ يعني هذا أنّ المعالج يمكنه معالجة العناوين التي تخزَّن على 64 بت وتحديدًا تكون سعة السجلات 64 بِتّ، وهو موضوع سنتناوله في مقال لاحق من هذه السلسلة.
يعني هذا أولًا أنّ جميع المؤشرات يجب أن تكون بحجم 64 بِتّ حتى تتمكن من تمثيل أيّ عنوان محتمل في النظام، لكن عندها يجب على منفّذِي النظام system implementers تحديد حجم الأنواع الأخرى، في حين ينتشر استخدام نموذجَين شائعَين على نطاق واسع كما هو موضح في الجدول التالي:
| النوع | الحجم الأدنى وفق معيار C99 بواحدة البِتّ | الحجم الشائع LP64 | الحجم الشائع في نظام التشغيل ويندوز |
|---|---|---|---|
| char | 8 | 8 | 8 |
| short | 16 | 16 | 16 |
| int | 16 | 32 | 32 |
| long | 32 | 64 | 32 |
| long long | 64 | 64 | 64 |
| المؤشرات Pointers | حسب التنفيذ | 64 | 64 |
يمكنك ملاحظة أنه في نموذج long pointer 64 أي المؤشرالطويل 64 -أو LP64 اختصارًا- يحدَّد حجم قيم المتغير من نوع Long بـ 64 بِتّ، وهذا يختلف عن نموذج 32 بِتّ الذي عرضناه سابقًا، إذ يستخدَم نموذج LP64 في أنظمة UNIX على نطاق واسع؛ أما في النموذج الآخر، فيبقى حجم المتغير من نوع long بقيمة 32 بت، وهذا يحافظ على أقصى قدر ممكن من التوافق مع الشيفرة البرمجية بنظام 32، إذ يُستخدَم هذا النموذج في نظام ويندوز الذي يدعم 64 بِتّ.
تكمن أسباب وجيهة خلف عدم زيادة حجم المتغير من نوع int إلى 64 بِتّ في أيّ من النموذجين، فإذا زاد حجم هذا المتغير إلى 64 بِتّ، فلن تترك للمبرمجين أيّ طريقة للحصول على متغير بحجم 32 بِتّ، وستكون الطريقة الوحيدة هي إعادة تعريف المتغيرات من نوع short لتكون من نوع 32 بِتّ الأكبر.
يُعَدّ المتغير بحجم 64 بِتّ كبيرًا جدًا لدرجة أنه ليس مطلوبًا عمومًا لتمثيل العديد من المتغيرات، فنادرًا ما تتكرر الحلقات loops مثلًا عدد مرات أكبر من أن يتسع في متغير حجمه 32 بِتّ الذي يتسع لـ 4294967296 مرة، وعادةً ما تمثَّل الصور بثمانية بِتّات لكل من قيم الأحمر والأخضر والأزرق وثمانية بِتّات إضافية مخصصة للمعلومات الإضافية (قناة ألفا) ما مجموعه 32 بِتّ، وبالتالي سيؤدي استخدام متغير بحجم 64 بِتّ في كثير من الحالات إلى إهدار أول 32 بِتّ على الأقل إذا لم يُهدَر أكثر من ذلك، وليس هذا فحسب، وإنما حجم مصفوفة عدد صحيح integer يتضاعف بذلك أيضًا.
يعني هذا أنّ البرامج ستستهلك حجمًا أكبر من ذاكرة النظام دون أيّ تحسن يذكر في أدائه، وبالتالي حجمًا أكبر من ذاكرة التخزين المؤقت cache التي سنتحدث عنها بالتفصيل في مقال لاحق من هذه السلسلة، ولهذا السبب اختار نظام ويندوز الاحتفاظ بتخزين قيم المتغيرات من نوع long في 32 بت، فبما أنّ الكثير من واجهات API على نظام ويندوز قد كُتبَت في الأصل لاستخدام متغيرات من نوع long مخزَّنة على نظام 32 بِتّ، لذا لا تحتاج إلى بِتّات إضافية، مما سيوفر ذلك مساحةً مهدورةً كبيرةً في النظام دون الحاجة إلى إعادة كتابة كامل واجهة API.
إذا جربنا البديل المقترَح المتمثل في إعادة تعريف المتغير من نوع short ليكون متغيرًا يخزَّن على 32 بِتّ، فسيستطيع المبرمجون الذين يعملون على نظام 64 بِتّ تحديد هذا النوع للمتغيرات التي يعلمون أنها مرتبطة بقيم أصغر، ولكن عند العودة إلى نظام 32 بِتّ، فسيكون متغير short نفسه الذي حددوه الآن بحجم 16 بِتّ فقط، وهي قيمة تجاوزوها بمراحل كبيرة عمليًا، أي 210 = 65536.
سيحقق جعل المبرمج يطلب متغيرات أكبر حجمًا عندما يعلم أنه سيحتاج إليها توازنًا فيما يتعلق بمخاوف قابلية النقل وإهدار المساحة في الأنظمة الثنائية.
مؤهلات الأنواع
يتحدث معيار اللغة C أيضًا عن بعض المؤهلات qualifiers لأنواع المتغيرات، إذ يشير المؤهل const مثلًا إلى أنّ المتغير لن تُعدَّل قيمته الأصلية أبدًا، والمؤهل volatile يقترح على المصرِّف بأنّ قيمة المتغير قد تتغير بعيدًا عن تدفق تنفيذ البرنامج، لذا يجب أن يحرص المصرِّف على عدم إعادة ترتيب الوصول إليه بأيّ شكل من الأشكال، كما يُعَدّ كل من مؤهل المؤشَّر signed ومؤهل غير المؤشَّر unsigned أنهما المؤهلَين الأهم على الأرجح، فهما يحدِّدان فيما إذا كان يُسمَح للمتغير بأن يأخذ قيمةً سالبةً أم لا، وسنتناول هذا بالتفصيل لاحقًا. الغرض من جميع المؤهلات هو تمرير معلومات إضافية للمصرِّف حول كيفية استخدامِه للمتغير، ويعني هذا أمرَين وهما أنّ المصرِّف قادر على التحقق مما إذا انتهكت القواعد التي وضعتها بنفسك مثل الكتابة في متغير قيمته ثابتة const، وقادر على إجراء تحسينات بناءً على المعلومات الإضافية، وسندرس هذا في مقالات لاحقة من هذه السلسلة.
الأنواع المعيارية
يدرك واضعو معيار C99 أنّ كل هذه القواعد والأحجام ومخاوف توفر قابلية للنقل قد تصبح مربكةً جدًا، ولتسهيل الأمر فقد قدموا في المعيار سلسلةً من الأنواع الخاصة التي تحدِّد الخصائص المضبوطة للمتغير، وتُحدَّد في الترويسة <stdint.h> وصيغتها qtypes_t، إذ يرمز المحرف q إلى المؤهل ويرمز type إلى النوع الأساسي، في حين يرمز المحرف s إلى الحجم بواحدة البِتّ وt- هو امتداد يشير إلى أنك تستخدِم الأنواع المعرَّفة في معيار C99.
تشير الصيغة uint8_t مثلًا إلى عدد صحيح غير مؤشَّر يخزَّن على 8 بِتّات بالضبط، وقد عُرِّفَت العديد من الأنواع الأخرى، إذ يمكنك الاطلاع على القائمة الكاملة المفصَّلة في مقطع المكتبة المعيارية 17.8 لمعيار C99 أو في ملف الترويسة الموجود بصورة مشفَّرة، كما إنّ توفير هذه الأنواع هي مهمة النظام الذي يطبق معيار C99 بأن يحدِّد لها الأنواع ذات الحجم الملائم على النظام المستهدَف، فمثلًا توفِّر مكتبات النظام هذه الترويسات في نظام التشغيل لينكس.
لاحظ أنّ معيار C99 فيه عوامل مساعدة لتحقيق قابلية النقل لـ printf، إذ يمكن استخدام وحدات ماكرو PRI macros في <inttypes.h> على أساس عوامل محددة للأنواع التي حُدِّدت أحجامها، وكما ذكرنا يمكنك الاطلاع على المعلومات كاملةً في المعيار أو باستخراج الترويسات.
التطبيق العملي للأنواع
نرى في النموذج التالي الذي يمثِّل التحذيرات التي ترد عندما لا تتطابق الأنواع مثالًا على فرض الأنواع قيودًا تحدِّد أيّ العمليات المتاح تنفيذها على المتغير وكيف يستعين المصرِّف بهذه المعلومات ليعرض تحذيرًا عند استخدام المتغيرات بطريقة تخالف تلك القيود، إذ نبدأ في هذه الشيفرة البرمجية بإسناد قيمة عدد صحيح integer للمتغير char، وبما أنّ حجم المتغير char أصغر، فسنفقد القيمة الصحيحة للعدد الصحيح integer.
نحاول بعدها تعيين مؤشر pointer للمتغير char يشير إلى الذاكرة التي حددنا بأنها عدد صحيح integer، ويمكن تنفيذ هذه العملية، لكنها ليست آمنةً، لذا نُفِّذ المثال الأول على جهاز معالجه بينتيوم Pentium ذو 32 بِتّ، وأعيدَت القيمة الصحيحة، لكن يبلغ حجم المؤشر 64 بتّ -أي 8 بايت- في نظام معالجه إيتانيوم Itanium ذو 64 بِتّ كما هو موضح في المثال الثاني، ولكن حجم العدد الصحيح integer يبلغ 4 بايت فقط، وبالطبع لن تتسع 8 بايت في 4 بايت.
يمكننا محاولة خداع المصرف بتحويل القيمة قبل إسنادها، ولاحظ أننا في هذه الحالة فاقمنا المشكلة عندما نفَّذنا هذا التحويل وتجاهلنا تحذير المصرف، لأنّ المتغير الأصغر لا يمكنه الاحتفاظ بجميع المعلومات الواردة من المؤشر، فنتلقى في النهاية عنوانًا غير صالح.
1 /* * types.c */ 5 #include <stdio.h> #include <stdint.h> int main(void) { 10 char a; char *p = "hello"; int i; 15 // نقل متغير كبير إلى متغير أصغر منه i = 0x12341234; a = i; i = a; printf("i is %d\n", i); 20 // نقل المؤشر ليشير إلى متغير من نوع integer printf("p is %p\n", p); i = p; // الخداع بإجراء التحويلات 25 i = (int)p; p = (char*)i; printf("p is %p\n", p); return 0; 30 }
1 $ uname -m i686 $ gcc -Wall -o types types.c 5 types.c: In function 'main': types.c:19: warning: assignment makes integer from pointer without a cast $ ./types i is 52 10 p is 0x80484e8 p is 0x80484e8 $ uname -m ia64 15 $ gcc -Wall -o types types.c types.c: In function 'main': types.c:19: warning: assignment makes integer from pointer without a cast types.c:21: warning: cast from pointer to integer of different size 20 types.c:22: warning: cast to pointer from integer of different size $ ./types i is 52 p is 0x40000000000009e0 25 p is 0x9e0
تمثيل الأعداد
سنشرح كيفية تمثيل الأعداد بمختلف مجالاتها مثل الأعداد السالبة والأعداد العشرية وغيرهما.
القيم السلبية
نميِّز العدد السالب في نظامنا العشري الحديث بوضع علامة الطرح - قبله؛ أما عندما نستخدِم النظام الثنائي، فعلينا اتباع أسلوب مختلف عند الإشارة إلى الأرقام السالبة، إذ يوجد نظام وحيد شائع استخدامه في العتاد الصلب الحديث، لكن معيار C99 يحدِّد ثلاثة أساليب مقبولة لتمثيل القيمة السلبية.
بت الإشارة Sign Bit
أبسط طريقة هي تخصيص بت واحد من العدد يشير إلى قيمة سالبة أو موجبة حسب هل هو محدَّد أم لا، وهذا مشابه للنهج الرياضي الذي يبين قيمة العدد بإشارتي + و-، إذ يُعَدّ هذا منطقيًا نوعًا ما، وقد مثّلت بعض أجهزة الحاسوب الأولية أعدادًا سالبةً بهذه الطريقة، لكن يتيح استخدام الأعداد الثنائية بعض الاحتمالات الأخرى التي تسهِّل عمل مصممي العتاد الصلب.
لاحظ أنّ القيمة 0 قد أصبح لها الآن قيمتان مكافئتان، واحدة حُدِّد فيها بِتّ إشارة وواحدة دون تحديده، وقد يُشار أحيانًا إلى هذه القيم بـ 0+ و 0- على التوالي.
المتمم الأحادي One's complement
يطبِّق نهج المتمِّم الأحادي العملية not على العدد الموجب لتمثيل العدد السالب، لذا تمثَّل القيمة 90- (0x5A-) مثلًا بـ 10100101 = 01011010~.
لاحظ أن العامِل ~ هو عامِل في اللغة C الذي يطبق عامِل NOT على القيمة، كما يدعى أحيانًا بعامِل المتمم الأحادي لأسباب صارت معروفة لدينا الآن.
الميزة الأكبر في هذا النظام هي أنه لا يشترط تطبيق منطق خاص عند إضافة عدد سالب إلى عدد موجب، باستثناء أنه يجب إضافة أيّ حمل carry إضافي متبقي إلى القيمة النهائية، لذا تأمل الجدول التالي:
| النظام العشري | النظام الثنائي | العملية |
|---|---|---|
| 90- | 10100101 | + |
| 100 | 01100100 | |
| --- | -------- | |
| 10 | 00001001 1 | 9 |
| 00001010 | 10 |
إذا أضفت البتات الواحد تلو الآخر، فستجد أنه سينتج لديك في النهاية بِتّ حمل carry bit الموضَّح في الجدول، وستنتج لدينا القيمة الصحيحة 10 بإضافته مجددًا إلى العدد الأصلي.
مجددًا لا تزال لدينا مشكلة تمثيل الصِفرين، ولا يوجد حاسوب حديث يستخدِم المتمم الأحادي، والسبب الرئيسي في ذلك وجود نظام أفضل.
المتمم الثنائي Two's Complement
يتشابه المتمم الثنائي تمامًا مع المتمم الأحادي، باستثناء أنّ التمثيل السالب يضاف إليه واحد ونتجاهل أيّ بِتّات حمل متبقية، فإذا طبقناه على المثال السابق، فسنمثِّل العدد 90- وفق ما يلي:
~01011010+1=10100101+1 = 10100110
يعني هذا أنّ هناك تماثلًا غريبًا بعض الشيء في الأعداد التي يمكن تمثيلها؛ ففي العدد الصحيح integer مثلًا الذي يخزَّن على 8 بِتّ لدينا 82 = 256 قيمة ممكنة، كما يمكننا تمثيل 127- في نهج تمثيل بِتّ الإشارة بواسطة 127، لكن يمكننا تمثيل 127- في نظام المتمم الثنائي بواسطة 128 لأننا أزلنا مشكلة وجود صفرين، وضَع في الحسبان أنّ الصفر السالب هو (1 + 00000000~) = (1 + 11111111) = 00000000، ولاحظ تجاهل بِتّ الحمل.
| النظام العشري | النظام الثنائي | OP العملية |
|---|---|---|
| 90- | 10100110 | + |
| 100 | 01100100 | |
| --- | -------- | |
| 10 | 00001010 |
لا بدّ أنك لاحظت أنّ تطبيق المتمم الثنائي لن يُحيج مصممي العتاد الصلب إلا إلى توفير عمليات منطقية لدارات الإضافة، إذ يمكن إجراء عملية الطرح عن طريق متمم ثنائي ينفي القيمة المراد طرحها ثم يضيف القيمة الجديدة، وبالمثل يمكنك تنفيذ عملية الضرب بالجمع المتكرر وعملية القسمة بالطرح المتكرر. وبالتالي يختزل المتمم الثنائي جميع العمليات الحسابية البسيطة بعملية الجمع، ومن الجدير بالذكر أنه تستخدِم جميع الحواسيب الحديثة تمثيل المتمم الثنائي.
امتداد الإشارة Sign-extension
بناءً على صيغة المتمم الثنائي، عند زيادة حجم القيمة المؤشَّرة signed value، من المهم أن تمدَّد إشارة sign-extended البتات الإضافية، أي المنسوخة من البِتّ الأولي للقيمة الحالية، إذ تمثَّل قيمة العدد الصحيح 10- من نوع int المخزَّن على 32 بت في المتمم الثنائي في النظام الثنائي عبى سبيل المثال بالعدد 111111111111111111111111110110، فإذا أردنا تحويله إلى عدد صحيح من نوع long long int مخزَّن على 64 بِتّ، فعلينا أن نحرص على تعيين الرقم 1 للـ 32 بِتّ الإضافية للاحتفاظ بالإشارة نفسها للعدد الأصلي.
بفضل المتمم الثنائي، يكفي أخذ البِتّ الأولي من قيمة الخرج exiting value واستبدال جميع البتات المضافة بهذه القيمة، ويشار إلى هذه العمليات باسم امتداد الإشارة، وعادةً يتعامل معها المصرِّف في الحالات المحدَّدة في معيار اللغة، مع توفير المعالج عمومًا تعليمات خاصة لأخذ قيمة وتمديد إشارتها إلى قيمة أكبر.
الأعداد العشرية Floating Point
تحدثنا حتى الآن عن الأعداد الصحيحة integer أو الأعداد الكاملة فقط، وتسمى فئة الأعداد التي يمكن أن تمثِّل القيم العشرية بالأعداد العشرية.
نحتاج لإنشاء عدد عشري إلى طريقة لتمثيل مفهوم الجزء العشري في النظام الثنائي، ويُعرف النظام الأشيع الذي يحقق ذلك بمعيار الأعداد العشرية IEEE-754 لأن من نشره كان معهد مهندسي الكهرباء والإلكترون، كما يُعَدّ النظام بسيط للغاية من ناحية المفهوم، وهو مشابه إلى حد ما للصيغة العلمية scientific notation.
قد تمثَّل القيمة 123.45 عمومًا في الصيغة العلمية بالصيغة 1.2345*102، إذ نسمي 1.2345 الجزء المعنوي significand (أو الجزء الأهم الأساسي الذي له أهمية)؛ أما 10 فهو الأساس radix و 2 هو الأُس exponent.
نفكك البتات المتاحة في نموذج العدد العشري IEEE لنمثِّل الإشارة والجزء العشري وأس العدد العشري، إذ يمثَّل العدد العشري بالصيغة: "الإشارة × الجزء المعنوي × الأس2"، ويعادل بِتّ الإشارة إما 1 أو 1-، وبما أننا نعمل في النظام الثنائي، فسيكون لدينا دائمًا الأساس الضمني 2، كما تتنوع أحجام قيمة العدد العشري، وسندرس في الفقرة التالية القيمة التي تخزَّن على 32 بت فقط، وكلما زاد عدد البتات حظينا بدقة أكبر.
| الإشارة | الأس | الجزء المعنوي/الجزء العشري |
|---|---|---|
| S | EEEEEEEE | MMMMMMMMMMMMMMMMMMMMMMM |
العامل المهم الآخر هو انحياز bias الأس، إذ يجب أن يمثِّل الأس القيم الموجبة والسالبة، وبالتالي تُطرَح القيمة الضمنية للعدد 127 من الأس، إذ يحتوي الأس 0 مثلًا على حقل أس يساوي 127، في حين يمثِّل 128 العدد 1 ويمثل 126 العدد 1-.
يضيف كل بِتّ من الجزء المعنوي مزيدًا من الدقة إلى القيم التي يمكننا تمثيلها، وضَع في الحسبان تمثيل الصيغة العلمية للقيمة 198765، إذ يمكننا كتابة هذا بالصيغة 1.98765x106، الذي يقابل التمثيل التالي:
| 10-5 | 10-4 | 10-3 | 10-2 | 10-1 | . | 100 |
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | . | 1 |
يتيح كل رقم إضافي مجالًا أكبر من القيم العشرية التي يمكننا تمثيلها، إذ يزيد كل رقم بعد الفاصلة العشرية من دقة العدد بمقدار 10 مرات في النظام العشري، فيمكننا مثلًا تمثيل 0.0 بـ 0.9 -أي 10 قيم- برقم واحد بعد الفاصلة عشرية، و0.00 بـ 0.99 -أي 100 قيمة- برقمين، وهكذا؛ أما في النظام الثنائي، فبدلًا من أن يمنحنا كل رقم إضافي دقة أكبر بعشر أضعاف، لا نحظى إلا بضعفَي الدقة كما هو موضَّح في الجدول التالي، ويعني هذا أنّ التمثيل الثنائي الخاص لا يوجّهنا دائمًا بطريقة مباشرة إلى التمثيل العشري.
| 10-5 | 10-4 | 10-3 | 10-2 | 10-1 | . | 100 |
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | . | 1 |
لا تكون دقة كسورنا كبيرةً جدًا باستخدام بِتّ واحد فقط للدقة، فلا يسعنا إلا أن نقول أنّ الكسر إما 0 أو 0.5، فإذا أضفنا بِتًّا آخرًا للدقة، فيمكننا الآن القول أن القيمة العشرية هي إما 0 أو 0.25 أو 0.5 أو 0.75. ومع إضافة بِتّ آخر للدقة يمكننا الآن تمثيل القيم 0، 0.125، 0.25، 0.375، 0.5، 0.625، 0.75، 0.875.
وبالتالي فكلما زدنا عدد البِتّات حظينا بدقة أكبر، لكن بما أنّ مجال الأعداد المحتملة غير محدود، فلن تكفي البِتَات أبدًا لتمثيل أية قيمة محتمَلة، فإذا كان لدينا بِتّين فقط للدقة على سبيل المثال، وأردنا تمثيل القيمة 0.3، فلا يمكننا القول إلا أنها أقرب إلى 0.25، وطبعًا هذا غير كاف في معظم التطبيقات، لكن عندما يكون لدينا 22 بِتّ للجزء المعنوي، فسنحظى بدقة أفضل بكثير، لكن لا يزال ذلك غير كاف في معظم التطبيقات.
تزيد قيمة متغير من نوع double عدد بتات الجزء المعنوي إلى 52 بت، كما أنها تزيد مجال قيم الأس أيضًا، كما تخصص بعض الأجهزة 84 بِتّ للعدد العشري، و64 بِتّ للجزء المعنوي، إذ تتيح 64 بِتّ تلك دقةً هائلةً لا بدّ أن تكون مناسبةً لجميع التطبيقات،لشمهم باستثناء التطبيقات شديدة التعقيد والتي تحتاج حجمًا أكبر ( هل هذا كافٍ لتمثيل طول أقل من حجم الذرة؟).
1 $ cat float.c #include <stdio.h> int main(void) 5 { float a = 0.45; float b = 8.0; double ad = 0.45; 10 double bd = 8.0; printf("float+float, 6dp : %f\n", a+b); printf("double+double, 6dp : %f\n", ad+bd); printf("float+float, 20dp : %10.20f\n", a+b); 15 printf("dobule+double, 20dp : %10.20f\n", ad+bd); return 0; } 20 $ gcc -o float float.c $ ./float float+float, 6dp : 8.450000 double+double, 6dp : 8.450000 25 float+float, 20dp : 8.44999998807907104492 dobule+double, 20dp : 8.44999999999999928946 $ python Python 2.4.4 (#2, Oct 20 2006, 00:23:25) 30 [GCC 4.1.2 20061015 (prerelease) (Debian 4.1.1-16.1)] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> 8.0 + 0.45 8.4499999999999993 35
يُعَدّ النموذج السابق مثالًا عمليًا لما تحدثنا عنه، ولاحظ أنه تتطابق الإجابتان بالنسبة للأجزاء العشرية الستة الافتراضية لتحقيق الدقة التي حددناها في printf، وذلك لأن عملية تقريبهما نفِّذت تنفيذًا صحيحًا، لكن عندما يُطلب منك إعطاء نتائج بدقة أكبر ولتكن في هذه الحالة 20 منزلة عشرية، فسنجد أنها تبدأ في الاختلاف.
منحتنا الشيفرة البرمجية التي تستخدِم النوع double نتيجةً أدق، لكنها لا تزال غير صحيحة كليًا، كما أننا نجد أنّ المبرمجين الذين لا يتعاملون بوضوح مع القيم من نوع float لا يزالون يواجهون مشاكل في دقة المتغيرات.
القيم الموحدة Normalised Values
يمكننا تمثيل قيمة بعدة أساليب مختلفة في الصيغة العلمية مثل 10023x100 = 1002.3x101 = 100.23x102، وبالتالي نعرّف صيغة التوحيد بأنه الصيغة التي يكون فيها 1/radix <= significand < 1، إذ تعني radix الأساس وتعني significand الجزء المعنوي، والعدد الموحَّد normalized number هو العدد المكتوب بالصيغة العلمية scientific notation مع رقم عشري واحد غير صفري على الأقل بعد الفاصلة.
يضمن هذا في النظام الثنائي أن يكون البِتّ الذي يقع أقصى اليسار leftmost bit من الجزء المعنوي دائمًا 1، فعند معرفتنا لذلك، يمكننا الحصول على بِتّ إضافي للدقة حسب ما ورد في المعيار أنه عندما يكون البت الأيسر 1 يكون ضمنيًا.
| العملية الحسابية | الأس | 2-5 | 2-4 | 2-3 | 2-2 | 2-1 | . | 20 |
|---|---|---|---|---|---|---|---|---|
| 0.375 = 1* (0.25+0.125) | 02 | 0 | 0 | 1 | 1 | 0 | . | 0 |
| 0.375= 5. * (0.5+0.25) | 1-2 | 0 | 0 | 0 | 1 | 1 | . | 0 |
| 0.375= 0.25 * (1+0.5) | 2-2 | 0 | 0 | 0 | 0 | 1 | . | 1 |
كما ترى في المثال السابق، يمكننا جعل القيمة قيمة موحَّدة من خلال تحريك البِتّات للأمام طالما أننا نعوِّض عن ذلك بزيادة الأس.
مهارات التوحيد
من المشكلات الشائعة التي يواجهها المبرمجون هي العثور على أول بِتّ ضبط في مجموعة البِتّات bitfield، ولنأخذ مجموعة البتات 0100 مثالًا، فعند البدء من اليمين، يكون بِتّ الضبط الأول هو البِتّ 2، إذ نبدأ من الصفر كما هو معتاد.
الطريقة المعيارية للعثور على هذه القيمة هي الإزاحة إلى اليمين والتحقق مما إذا كان البِتّ الأول هو 1 أي بت الضبط، ثم إنهاء العملية أو تكرارها، وتُعَدّ هذه عمليةً بطيئةً، فإذا كان طول مجموعة البِتّات 64 بِتّ وكان بِتّ الضبط هو الأخير فقط، فيجب أن تمر بجميع البتات الثلاثة والستين التي تسبقها.
لكن إذا كانت قيمة مجموعة البتات هذه هي الجزء المعنوي لعدد عشري وكان علينا توحيدها، فسنعرف من قيمة الأس عدد مرات إزاحتها، كما تضمَّن عملية التوحيد عمومًا في وحدة عتاد العدد العشري على المعالج، لذا تؤدَّى بسرعة كبيرة، وعادةً أسرع بكثير من عمليات الإزاحة والاختبار المتكررة.
يوضِّح البرنامج التالي طريقتين للعثور على أول بِتّ ضبط متَّبعتَين على معالج إتانيوم. إذ يدعم المعالج إتانيوم -مثل حال معظم معالجات الخوادم- نوع العدد العشري الموسَّع الذي يخزَّن على 80 بِتّ، والجزء المعنوي الذي يخزن على 64 بِتّ، ويعني هذا أنّ نوع unsigned long يتوافق بدقة في الجزء المعنوي لنوع long double، فعندما تحمَّل القيمة توحَّد، وبالتالي من خلال قراءة قيمة الأس مطروحًا منها انحياز 16 بِتّ يمكننا رؤية مدى انزياحها.
1 #include <stdio.h> int main(void) { 5 // في التمثيل الثنائي = 0000 0000 0000 1000 // عدد البتات 3210 7654 1098 5432 int i = 0x8000; int count = 0; while ( !(i & 0x1) ) { 10 count ++; i = i >> 1; } printf("First non-zero (slow) is %d\n", count); 15 // توحَّد هذه القيمة عندما تُحمَّل long double d = 0x8000UL; long exp; // تعليمات "الحصول على أس العدد العشري" في معالج إتانيوم 20 asm ("getf.exp %0=%1" : "=r"(exp) : "f"(d)); // الأس متضمنًا الانزياح printf("The first non-zero (fast) is %d\n", exp - 65535); 25 }
خلاصة الأفكار السابقة
نستخرج مكونات العدد العشري ونطبع القيمة التي يمثلها في نموذج الشيفرة البرمجية التالية، إذ سنحرز نتيجةً فقط عندما تكون القيمة عددًا عشريًا بحجم 32 بِتّ بصيغة المعيار IEEE، وهذا شائع في معظم المعماريات من نوع float أي عدد عشري.
1 #include <stdio.h> #include <string.h> #include <stdlib.h> 5 /* 2^n إرجاع */ int two_to_pos(int n) { if (n == 0) return 1; 10 return 2 * two_to_pos(n - 1); } double two_to_neg(int n) { 15 if (n == 0) return 1; return 1.0 / (two_to_pos(abs(n))); } 20 double two_to(int n) { if (n >= 0) return two_to_pos(n); if (n < 0) 25 return two_to_neg(n); return 0; } /* مراجعة بعض أجزاء الذاكرة للمتغير "m" الذي هو الجزء المعنوي 30 للعدد العشري بحجم 24 بت، نبدأ بالمقلوب من البتات في أقصى اليمين دون أي سبب معين */ double calc_float(int m, int bit) { /* 23 بت؛ هذا ينهي العودية */ 35 if (bit > 23) return 0; /* إذا كان البت مضبوطًا، فهو يمثل القيمة 2/1^بت */ if ((m >> bit) & 1) 40 return 1.0L/two_to(23 - bit) + calc_float(m, bit + 1); /* وإلا انتقل إلى البت التالي */ return calc_float(m, bit + 1); } 45 int main(int argc, char *argv[]) { float f; int m,i,sign,exponent,significand; 50 if (argc != 2) { printf("usage: float 123.456\n"); exit(1); 55 } if (sscanf(argv[1], "%f", &f) != 1) { printf("invalid input\n"); 60 exit(1); } /* سنحتاج إلى خداع المصرف، كأننا بدأنا استخدام التحويلات فمثلًا (int)(f) ستجري تحويلًا فعليًا لنا 65 نريد الوصول إلى البتات الأولية، لذا ننسخها إلى متغير بنفس الحجم. */ memcpy(&m, &f, 4); /* بت الإشارة هو أول بت */ 70 sign = (m >> 31) & 0x1; /* الأس هو البتات الثمانية التي تلي بت الإشارة */ exponent = ((m >> 23) & 0xFF) - 127; 75 /* الجزء المعنوي يملأ المنازل العشرية، ويكون أول بت ضمنيًا 1 وبالتالي هو قيمة المعامل OR 24 بت. */ significand = (m & 0x7FFFFF) | 0x800000; /* اطبع قيمةً تمثل الأس */ 80 printf("%f = %d * (", f, sign ? -1 : 1); for(i = 23 ; i >= 0 ; i--) { if ((significand >> i) & 1) printf("%s1/2^%d", (i == 23) ? "" : " + ", 85 23-i); } printf(") * 2^%d\n", exponent); /* اطبع تمثيلًا كسريًا */ 90 printf("%f = %d * (", f, sign ? -1 : 1); for(i = 23 ; i >= 0 ; i--) { if ((significand >> i) & 1) printf("%s1/%d", (i == 23) ? "" : " + ", 95 (int)two_to(23-i)); } printf(") * 2^%d\n", exponent); /* حول هذا إلى قيمة عشرية واطبعه */ 100 printf("%f = %d * %.12g * %f\n", f, (sign ? -1 : 1), calc_float(significand, 0), two_to(exponent)); 105 /* اجرِ العملية الحسابية الآن */ printf("%f = %.12g\n", f, (sign ? -1 : 1) * 110 calc_float(significand, 0) * two_to(exponent) ); return 0; 115 }
وفيما يلي نموذج خرج القيمة 8.45 الذي درسناه سابقًا:
$ ./float 8.45 8.450000 = 1 * (1/2^0 + 1/2^5 + 1/2^6 + 1/2^7 + 1/2^10 + 1/2^11 + 1/2^14 + 1/2^15 + 1/2^18 + 1/2^19 + 1/2^22 + 1/2^23) * 2^3 8.450000 = 1 * (1/1 + 1/32 + 1/64 + 1/128 + 1/1024 + 1/2048 + 1/16384 + 1/32768 + 1/262144 + 1/524288 + 1/4194304 + 1/8388608) * 2^3 8.450000 = 1 * 1.05624997616 * 8.000000 8.450000 = 8.44999980927
نستخلص من هذا المثال فكرةً عن تسلل عدم الدقة إلى أعدادنا العشرية.
ترجمة -وبتصرّف- لقسم من الفصل Chapter 2. Binary and Number Representation من كتاب Computer Science from the Bottom Up.
اقرأ أيضًا
- المقال السابق: تعرف على نظام العد الثنائي Binary أساس الحوسبة
- المدخل الشامل لتعلم علوم الحاسوب
- النسخة العربية لكتاب: أنظمة التشغيل للمبرمجين
تعليقات
إرسال تعليق